希尔排序(C/C++/Java)

本章会对排序算法中的希尔排序进行图文详解，并给出C/C++/Java的实现。

希尔排序介绍

希尔排序(Shell Sort)是插入排序的一种，它是针对直接插入排序算法的改进。该方法又称缩小增量排序，因DL．Shell于1959年提出而得名。

希尔排序实质上是一种分组插入方法。它的基本思想是：对于n个待排序的数列，取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的记录放在同一个组中；然后，对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

希尔排序图文说明

1. 希尔排序代码(一)

/*
 * 希尔排序
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     n -- 数组的长度
 */
void shell_sort1(int a[], int n)
{
    int i,j,gap;

    // gap为步长，每次减为原来的一半。
    for (gap = n / 2; gap > 0; gap /= 2)
    {
        // 共gap个组，对每一组都执行直接插入排序
        for (i = 0 ;i < gap; i++)
        {
            for (j = i + gap; j < n; j += gap) 
            {
                // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
                if (a[j] < a[j - gap])
                {
                    int tmp = a[j];
                    int k = j - gap;
                    while (k >= 0 && a[k] > tmp)
                    {
                        a[k + gap] = a[k];
                        k -= gap;
                    }
                    a[k + gap] = tmp;
                }
            }
        }

    }
}

在上面的希尔排序中，首先要选取步长gap的值。选取了gap之后，就将数列分成了gap个组，对于每一个组都执行直接插入排序。在排序完所有的组之后，将gap的值减半；继续对数列进行分组，然后进行排序。重复这样的操作，直到gap<0为止。此时，数列也就是有序的了。

为了便于观察，我们将希尔排序中的直接插入排序独立出来，得到代码(二)。

2. 希尔排序代码(二)

/*
 * 对希尔排序中的单个组进行排序
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     n -- 数组总的长度
 *     i -- 组的起始位置
 *     gap -- 组的步长
 *
 *  组是"从i开始，将相隔gap长度的数都取出"所组成的！
 */
void group_sort(int a[], int n, int i,int gap)
{
    int j;

    for (j = i + gap; j < n; j += gap) 
    {
        // 如果a[j] < a[j-gap]，则寻找a[j]位置，并将后面数据的位置都后移。
        if (a[j] < a[j - gap])
        {
            int tmp = a[j];
            int k = j - gap;
            while (k >= 0 && a[k] > tmp)
            {
                a[k + gap] = a[k];
                k -= gap;
            }
            a[k + gap] = tmp;
        }
    }
}

/*
 * 希尔排序
 *
 * 参数说明：
 *     a -- 待排序的数组
 *     n -- 数组的长度
 */
void shell_sort2(int a[], int n)
{
    int i,gap;

    // gap为步长，每次减为原来的一半。
    for (gap = n / 2; gap > 0; gap /= 2)
    {
        // 共gap个组，对每一组都执行直接插入排序
        for (i = 0 ;i < gap; i++)
            group_sort(a, n, i, gap);
    }
}

下面以数列{80,30,60,40,20,10,50,70}为例，演示它的希尔排序过程(如下图)。

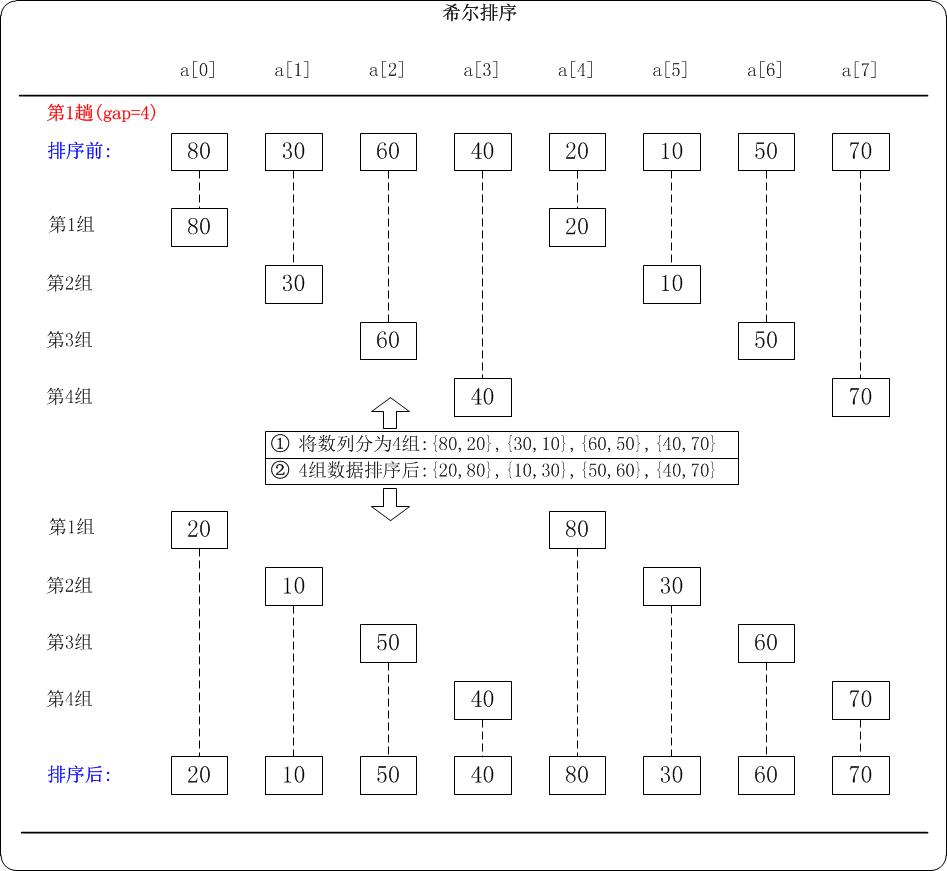
第1趟：(gap=4)

  • 当gap=4时,意味着将数列分为4个组： {80,20},{30,10},{60,50},{40,70}。 对应数列： {80,30,60,40,20,10,50,70}
  • 对这4个组分别进行排序，排序结果： {20,80},{10,30},{50,60},{40,70}。 对应数列： {20,10,50,40,80,30,60,70}

img

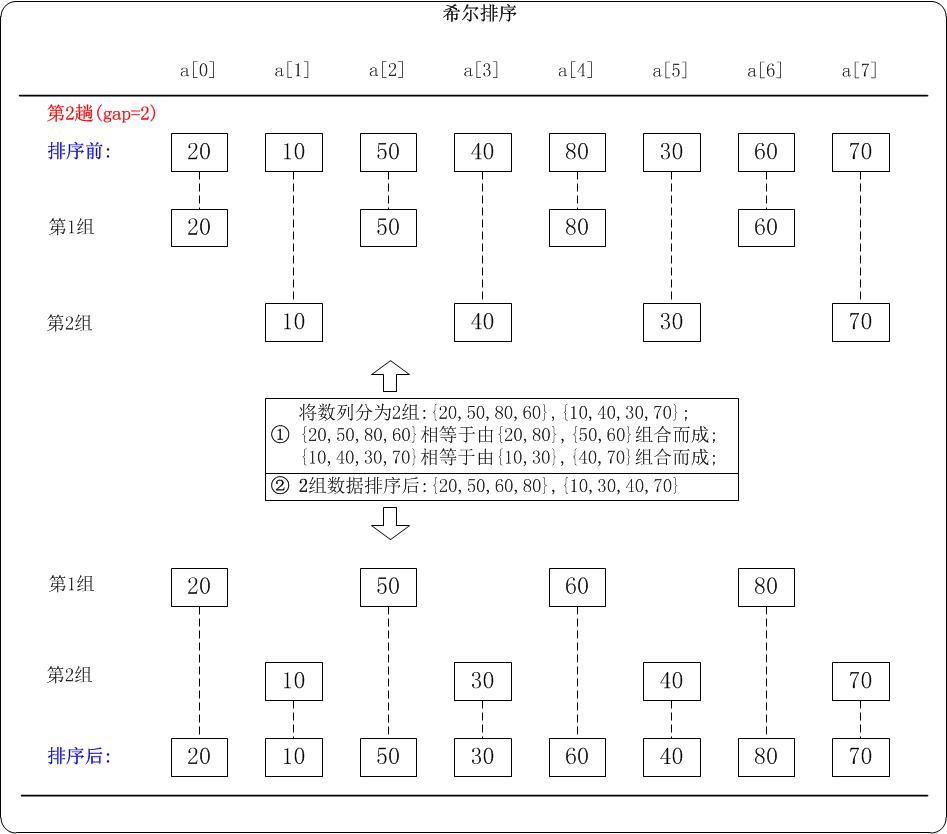
第2趟：(gap=2)

  • 当gap=2时,意味着将数列分为2个组：{20,50,80,60}, {10,40,30,70}。 对应数列： {20,10,50,40,80,30,60,70}
       注意：{20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。
                   {10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。
  • 对这2个组分别进行排序，排序结果：{20,50,60,80}, {10,30,40,70}。 对应数列： {20,10,50,30,60,40,80,70}

img

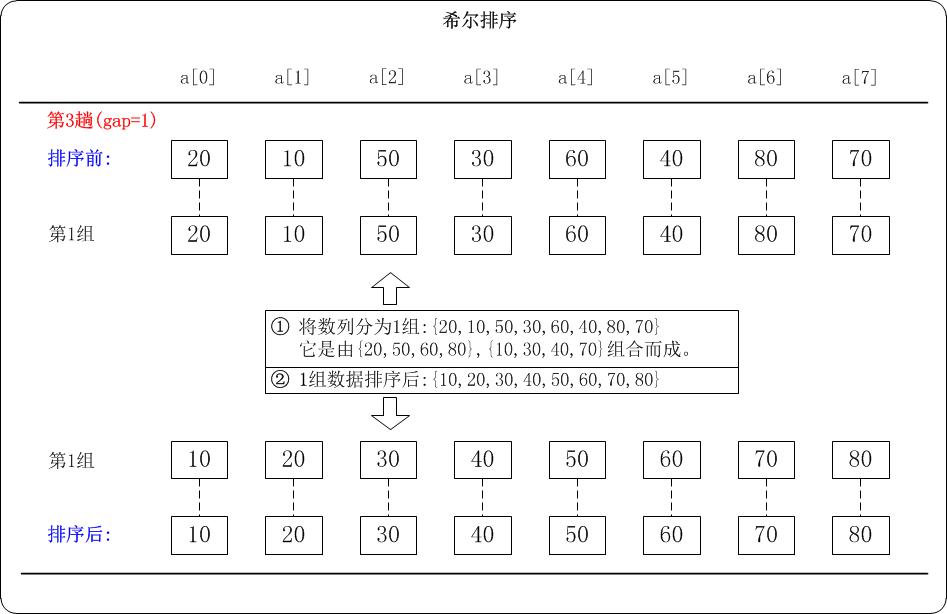
第3趟：(gap=1)

  • 当gap=1时,意味着将数列分为1个组：{20,10,50,30,60,40,80,70}。
    注意：{20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。
  • 对这1个组分别进行排序，排序结果：{10,20,30,40,50,60,70,80}

img

希尔排序的时间复杂度和稳定性

希尔排序时间复杂度

希尔排序的时间复杂度与增量(即，步长gap)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N2)，而Hibbard增量的希尔排序的时间复杂度为O(N3/2)。


希尔排序稳定性

希尔排序是不稳定的算法，它满足稳定算法的定义。对于相同的两个数，可能由于分在不同的组中而导致它们的顺序发生变化。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

希尔排序实现

  1. 希尔排序C实现 (shell_sort.c)
  2. 希尔排序C++实现 (ShellSort.cpp)
  3. 希尔排序Java实现 (ShellSort.java)
by skywang
Previous     Next