本章会对排序算法中的冒泡排序进行图文详解,并给出C/C++/Java的实现。
冒泡排序介绍
冒泡排序(Bubble Sort),又被称为气泡排序或泡沫排序。
它是一种较简单的排序算法。它会遍历若干次要排序的数列,每次遍历时,它都会从前往后依次的比较相邻两个数的大小;如果前者比后者大,则交换它们的位置。这样,一次遍历之后,最大的元素就在数列的末尾! 采用相同的方法再次遍历时,第二大的元素就被排列在最大元素之前。重复此操作,直到整个数列都有序为止!
冒泡排序图文说明
1. 冒泡排序C实现一
/*
* 冒泡排序
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
void bubble_sort1(int a[], int n)
{
int i,j;
for (i=n-1; i>0; i--)
{
// 将a[0...i]中最大的数据放在末尾
for (j=0; j<i; j++)
{
if (a[j] > a[j+1])
swap(a[j], a[j+1]);
}
}
}
下面以数列{20,40,30,10,60,50}为例,演示它的冒泡排序过程(如下图)。
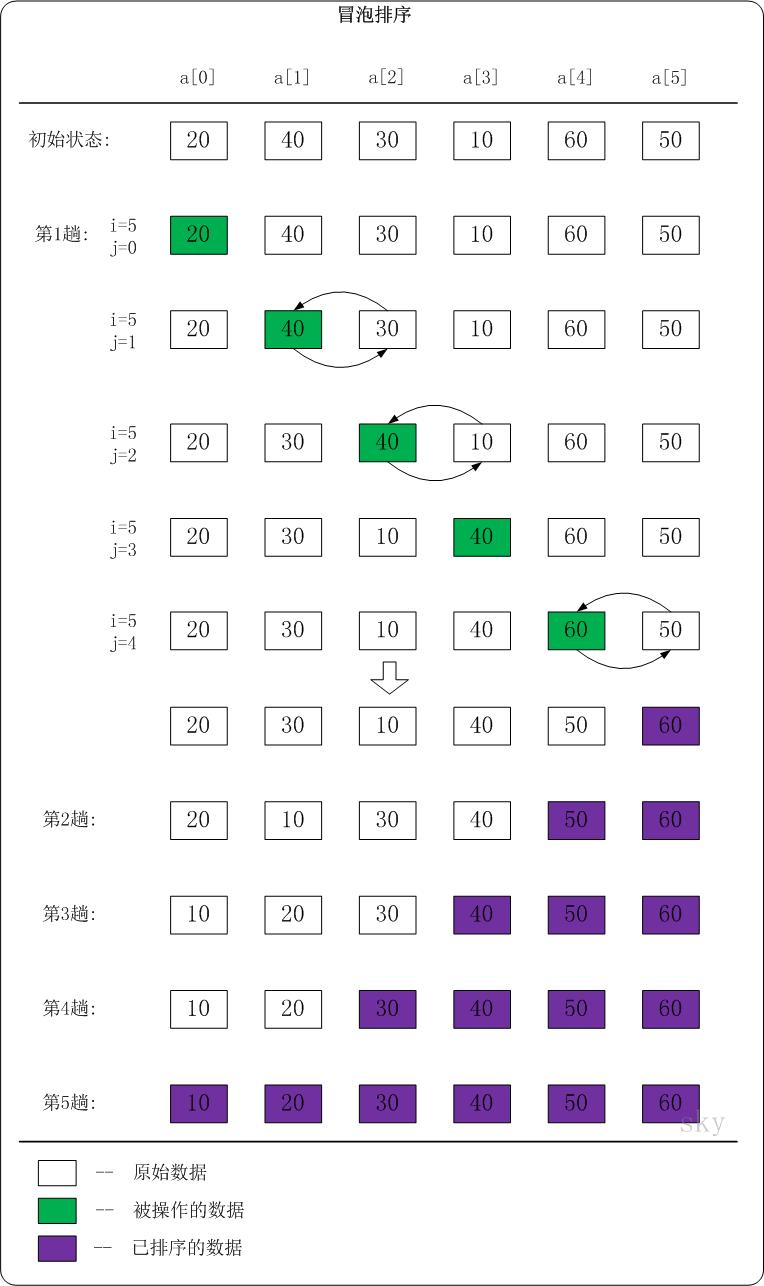
我们先分析第1趟排序
- 当i=5,j=0时,a[0]<a[1]。此时,不做任何处理!
- 当i=5,j=1时,a[1]>a[2]。此时,交换a[1]和a[2]的值;交换之后,a[1]=30,a[2]=40。
- 当i=5,j=2时,a[2]>a[3]。此时,交换a[2]和a[3]的值;交换之后,a[2]=10,a[3]=40。
- 当i=5,j=3时,a[3]<a[4]。此时,不做任何处理!
- 当i=5,j=4时,a[4]>a[5]。此时,交换a[4]和a[5]的值;交换之后,a[4]=50,a[3]=60。
于是,第1趟排序完之后,数列{20,40,30,10,60,50}变成了{20,30,10,40,50,60}。此时,数列末尾的值最大。
根据这种方法,
第2趟排序完之后,数列中a[5...6]是有序的。
第3趟排序完之后,数列中a[4...6]是有序的。
第4趟排序完之后,数列中a[3...6]是有序的。
第5趟排序完之后,数列中a[1...6]是有序的。
第5趟排序之后,整个数列也就是有序的了。
2. 冒泡排序C实现二
观察上面冒泡排序的流程图,第3趟排序之后,数据已经是有序的了;第4趟和第5趟并没有进行数据交换。
下面我们对冒泡排序进行优化,使它效率更高一些:添加一个标记,如果一趟遍历中发生了交换,则标记为true,否则为false。如果某一趟没有发生交换,说明排序已经完成!
优化后的C代码
/*
* 冒泡排序(改进版)
*
* 参数说明:
* a -- 待排序的数组
* n -- 数组的长度
*/
void bubble_sort2(int a[], int n)
{
int i,j;
int flag; // 标记
for (i=n-1; i>0; i--)
{
flag = 0; // 初始化标记为0
// 将a[0...i]中最大的数据放在末尾
for (j=0; j<i; j++)
{
if (a[j] > a[j+1])
{
swap(a[j], a[j+1]);
flag = 1; // 若发生交换,则设标记为1
}
}
if (flag==0)
break; // 若没发生交换,则说明数列已有序。
}
}
冒泡排序的时间复杂度和稳定性
冒泡排序时间复杂度
冒泡排序的时间复杂度是O(N2)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N),需要遍历多少次呢?N-1次!因此,冒泡排序的时间复杂度是O(N2)。
冒泡排序稳定性
冒泡排序是稳定的算法,它满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
冒泡排序实现
- 冒泡排序C实现 (bubble_sort.c)
- 冒泡排序C++实现 (BubbleSort.cpp)
- 冒泡排序Java实现 (BubbleSort.java)