前面分别通过C和C++实现了普里姆,本文介绍普里姆的Java实现。
目录
1. 普里姆算法介绍
2. 普里姆算法图解
3. 普里姆算法的代码说明
4. 普里姆算法的源码
普里姆算法介绍
普里姆(Prim)算法,是用来求加权连通图的最小生成树的算法。
基本思想
对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。
从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。
普里姆算法图解
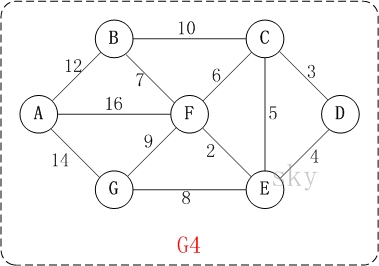
以上图G4为例,来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。
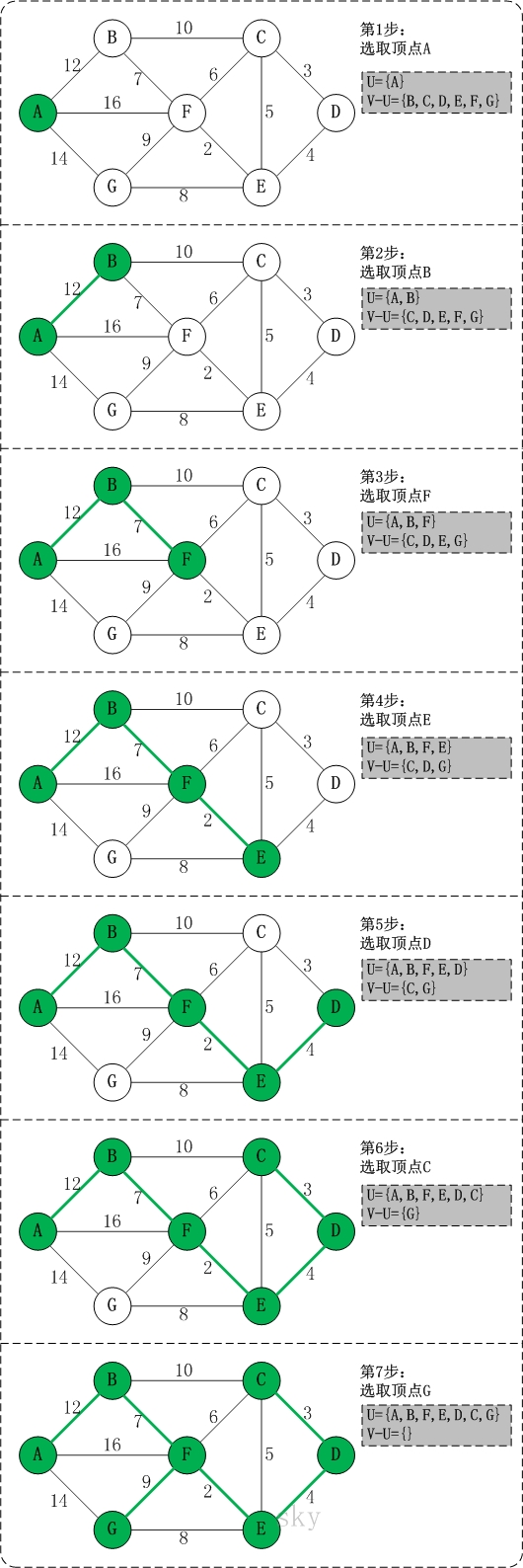
初始状态:V是所有顶点的集合,即V={A,B,C,D,E,F,G};U和T都是空!
第1步:将顶点A加入到U中。
此时,U={A}。
第2步:将顶点B加入到U中。
上一步操作之后,U={A}, V-U={B,C,D,E,F,G};因此,边(A,B)的权值最小。将顶点B添加到U中;此时,U={A,B}。
第3步:将顶点F加入到U中。
上一步操作之后,U={A,B}, V-U={C,D,E,F,G};因此,边(B,F)的权值最小。将顶点F添加到U中;此时,U={A,B,F}。
第4步:将顶点E加入到U中。
上一步操作之后,U={A,B,F}, V-U={C,D,E,G};因此,边(F,E)的权值最小。将顶点E添加到U中;此时,U={A,B,F,E}。
第5步:将顶点D加入到U中。
上一步操作之后,U={A,B,F,E}, V-U={C,D,G};因此,边(E,D)的权值最小。将顶点D添加到U中;此时,U={A,B,F,E,D}。
第6步:将顶点C加入到U中。
上一步操作之后,U={A,B,F,E,D}, V-U={C,G};因此,边(D,C)的权值最小。将顶点C添加到U中;此时,U={A,B,F,E,D,C}。
第7步:将顶点G加入到U中。
上一步操作之后,U={A,B,F,E,D,C}, V-U={G};因此,边(F,G)的权值最小。将顶点G添加到U中;此时,U=V。
此时,最小生成树构造完成!它包括的顶点依次是:A B F E D C G。
普里姆算法的代码说明
以"邻接矩阵"为例对普里姆算法进行说明,对于"邻接表"实现的图在后面会给出相应的源码。
1. 基本定义
public class MatrixUDG {
private char[] mVexs; // 顶点集合
private int[][] mMatrix; // 邻接矩阵
private static final int INF = Integer.MAX_VALUE; // 最大值
...
}
MatrixUDG是邻接矩阵对应的结构体。mVexs用于保存顶点,mEdgNum用于保存边数,mMatrix则是用于保存矩阵信息的二维数组。例如,mMatrix[i][j]=1,则表示"顶点i(即mVexs[i])"和"顶点j(即mVexs[j])"是邻接点;mMatrix[i][j]=0,则表示它们不是邻接点。
2. 普里姆算法
/*
* prim最小生成树
*
* 参数说明:
* start -- 从图中的第start个元素开始,生成最小树
*/
public void prim(int start) {
int num = mVexs.length; // 顶点个数
int index=0; // prim最小树的索引,即prims数组的索引
char[] prims = new char[num]; // prim最小树的结果数组
int[] weights = new int[num]; // 顶点间边的权值
// prim最小生成树中第一个数是"图中第start个顶点",因为是从start开始的。
prims[index++] = mVexs[start];
// 初始化"顶点的权值数组",
// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
for (int i = 0; i < num; i++ )
weights[i] = mMatrix[start][i];
// 将第start个顶点的权值初始化为0。
// 可以理解为"第start个顶点到它自身的距离为0"。
weights[start] = 0;
for (int i = 0; i < num; i++) {
// 由于从start开始的,因此不需要再对第start个顶点进行处理。
if(start == i)
continue;
int j = 0;
int k = 0;
int min = INF;
// 在未被加入到最小生成树的顶点中,找出权值最小的顶点。
while (j < num) {
// 若weights[j]=0,意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
if (weights[j] != 0 && weights[j] < min) {
min = weights[j];
k = j;
}
j++;
}
// 经过上面的处理后,在未被加入到最小生成树的顶点中,权值最小的顶点是第k个顶点。
// 将第k个顶点加入到最小生成树的结果数组中
prims[index++] = mVexs[k];
// 将"第k个顶点的权值"标记为0,意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
weights[k] = 0;
// 当第k个顶点被加入到最小生成树的结果数组中之后,更新其它顶点的权值。
for (j = 0 ; j < num; j++) {
// 当第j个节点没有被处理,并且需要更新时才被更新。
if (weights[j] != 0 && mMatrix[k][j] < weights[j])
weights[j] = mMatrix[k][j];
}
}
// 计算最小生成树的权值
int sum = 0;
for (int i = 1; i < index; i++) {
int min = INF;
// 获取prims[i]在mMatrix中的位置
int n = getPosition(prims[i]);
// 在vexs[0...i]中,找出到j的权值最小的顶点。
for (int j = 0; j < i; j++) {
int m = getPosition(prims[j]);
if (mMatrix[m][n]<min)
min = mMatrix[m][n];
}
sum += min;
}
// 打印最小生成树
System.out.printf("PRIM(%c)=%d: ", mVexs[start], sum);
for (int i = 0; i < index; i++)
System.out.printf("%c ", prims[i]);
System.out.printf("\n");
}
普里姆算法的源码
这里分别给出"邻接矩阵图"和"邻接表图"的普里姆算法源码。