前面分别介绍了拓扑排序的C和C++实现,本文通过Java实现拓扑排序。
目录
1. 拓扑排序介绍
2. 拓扑排序的算法图解
3. 拓扑排序的代码说明
4. 拓扑排序的完整源码和测试程序
拓扑排序介绍
拓扑排序(Topological Order)是指,将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。
这样说,可能理解起来比较抽象。下面通过简单的例子进行说明!
例如,一个项目包括A、B、C、D四个子部分来完成,并且A依赖于B和D,C依赖于D。现在要制定一个计划,写出A、B、C、D的执行顺序。这时,就可以利用到拓扑排序,它就是用来确定事物发生的顺序的。
在拓扑排序中,如果存在一条从顶点A到顶点B的路径,那么在排序结果中B出现在A的后面。
拓扑排序的算法图解
拓扑排序算法的基本步骤:
1. 构造一个队列Q(queue) 和 拓扑排序的结果队列T(topological);
2. 把所有没有依赖顶点的节点放入Q;
3. 当Q还有顶点的时候,执行下面步骤:
3.1 从Q中取出一个顶点n(将n从Q中删掉),并放入T(将n加入到结果集中);
3.2 对n每一个邻接点m(n是起点,m是终点);
3.2.1 去掉边<n,m>;
3.2.2 如果m没有依赖顶点,则把m放入Q;
注:顶点A没有依赖顶点,是指不存在以A为终点的边。
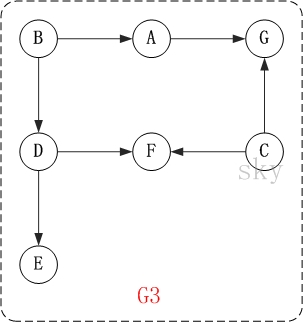
以上图为例,来对拓扑排序进行演示。
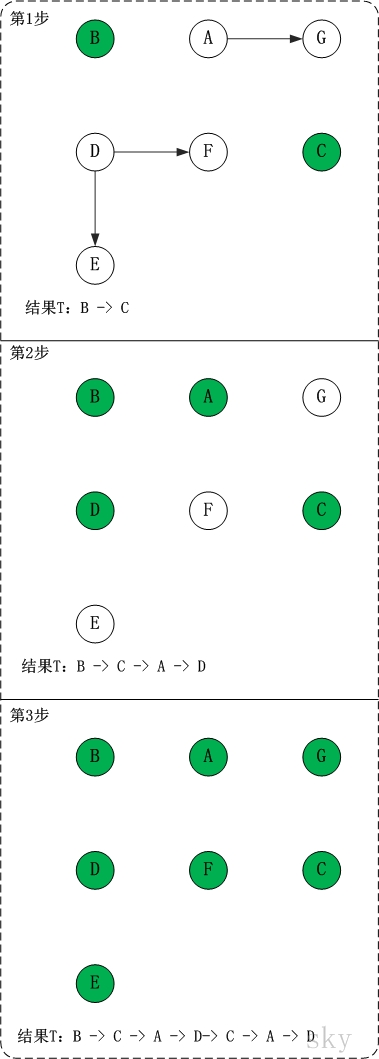
第1步:将B和C加入到排序结果中。
顶点B和顶点C都是没有依赖顶点,因此将C和C加入到结果集T中。假设ABCDEFG按顺序存储,因此先访问B,再访问C。访问B之后,去掉边<B,A>和<B,D>,并将A和D加入到队列Q中。同样的,去掉边<C,F>和<C,G>,并将F和G加入到Q中。
(01) 将B加入到排序结果中,然后去掉边<B,A>和<B,D>;此时,由于A和D没有依赖顶点,因此并将A和D加入到队列Q中。
(02) 将C加入到排序结果中,然后去掉边<C,F>和<C,G>;此时,由于F有依赖顶点D,G有依赖顶点A,因此不对F和G进行处理。
第2步:将A,D依次加入到排序结果中。
第1步访问之后,A,D都是没有依赖顶点的,根据存储顺序,先访问A,然后访问D。访问之后,删除顶点A和顶点D的出边。
第3步:将E,F,G依次加入到排序结果中。
因此访问顺序是:B -> C -> A -> D -> E -> F -> G
拓扑排序的代码说明
拓扑排序是对有向无向图的排序。下面以邻接表实现的有向图来对拓扑排序进行说明。
1. 基本定义
public class ListDG {
// 邻接表中表对应的链表的顶点
private class ENode {
int ivex; // 该边所指向的顶点的位置
ENode nextEdge; // 指向下一条弧的指针
}
// 邻接表中表的顶点
private class VNode {
char data; // 顶点信息
ENode firstEdge; // 指向第一条依附该顶点的弧
};
private VNode[] mVexs; // 顶点数组
...
}
(01) ListDG是邻接表对应的结构体。 mVexs则是保存顶点信息的一维数组。
(02) VNode是邻接表顶点对应的结构体。 data是顶点所包含的数据,而firstEdge是该顶点所包含链表的表头指针。
(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。 ivex是该节点所对应的顶点在vexs中的索引,而nextEdge是指向下一个节点的。
2. 拓扑排序
/*
* 拓扑排序
*
* 返回值:
* -1 -- 失败(由于内存不足等原因导致)
* 0 -- 成功排序,并输入结果
* 1 -- 失败(该有向图是有环的)
*/
public int topologicalSort() {
int index = 0;
int num = mVexs.size();
int[] ins; // 入度数组
char[] tops; // 拓扑排序结果数组,记录每个节点的排序后的序号。
Queue<Integer> queue; // 辅组队列
ins = new int[num];
tops = new char[num];
queue = new LinkedList<Integer>();
// 统计每个顶点的入度数
for(int i = 0; i < num; i++) {
ENode node = mVexs.get(i).firstEdge;
while (node != null) {
ins[node.ivex]++;
node = node.nextEdge;
}
}
// 将所有入度为0的顶点入队列
for(int i = 0; i < num; i ++)
if(ins[i] == 0)
queue.offer(i); // 入队列
while (!queue.isEmpty()) { // 队列非空
int j = queue.poll().intValue(); // 出队列。j是顶点的序号
tops[index++] = mVexs.get(j).data; // 将该顶点添加到tops中,tops是排序结果
ENode node = mVexs.get(j).firstEdge;// 获取以该顶点为起点的出边队列
// 将与"node"关联的节点的入度减1;
// 若减1之后,该节点的入度为0;则将该节点添加到队列中。
while(node != null) {
// 将节点(序号为node.ivex)的入度减1。
ins[node.ivex]--;
// 若节点的入度为0,则将其"入队列"
if( ins[node.ivex] == 0)
queue.offer(node.ivex); // 入队列
node = node.nextEdge;
}
}
if(index != num) {
System.out.printf("Graph has a cycle\n");
return 1;
}
// 打印拓扑排序结果
System.out.printf("== TopSort: ");
for(int i = 0; i < num; i ++)
System.out.printf("%c ", tops[i]);
System.out.printf("\n");
return 0;
}
说明:
(01) queue的作用就是用来存储没有依赖顶点的顶点。它与前面所说的Q相对应。
(02) tops的作用就是用来存储排序结果。它与前面所说的T相对应。