前面分别通过C和C++实现了二项堆,本章给出二项堆的Java版本。还是那句老话,三种实现的原理一样,择其一了解即可。
目录
第1部分 二项树的介绍
第2部分 二项堆的介绍
第3部分 二项堆的基本操作
第4部分 二项堆的Java实现(完整源码)
第1部分 二项树的介绍
二项树的定义
二项堆是二项树的集合。在了解二项堆之前,先对二项树进行介绍。
二项树是一种递归定义的有序树。它的递归定义如下:
(01) 二项树B0只有一个结点;
(02) 二项树Bk由两棵二项树B(k-1)组成的,其中一棵树是另一棵树根的最左孩子。
如下图所示:
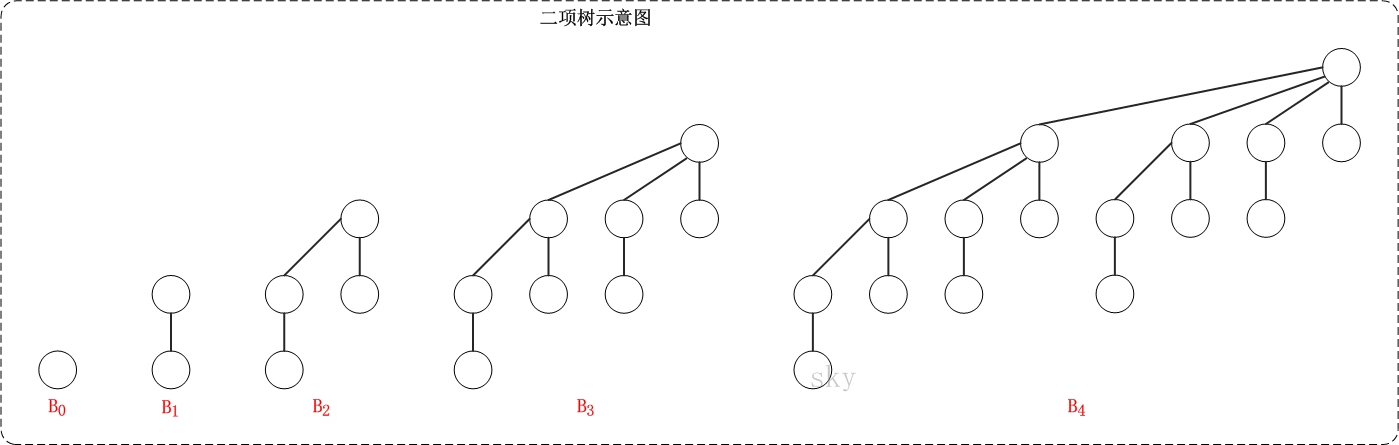
上图的B0、B1、B2、B3、B4都是二项树。对比前面提到的二项树的定义:B0只有一个节点,B1由两个B0所组成,B2由两个B1所组成,B3由两个B2所组成,B4由两个B3所组成;而且,当两颗相同的二项树组成另一棵树时,其中一棵树是另一棵树的最左孩子。
二项树的性质
二项树有以下性质:
[性质一] Bk共有2k个节点。
[性质二] Bk的高度为k。
[性质三] Bk在深度i处恰好有C(k,i)个节点,其中i=0,1,2,...,k。
[性质四] 根的度数为k,它大于任何其它节点的度数。
注意:树的高度和深度是相同的。关于树的高度的概念,《算法导论》中只有一个节点的树的高度是0,而"维基百科"中只有一个节点的树的高度是1。本文使用了《算法导论中》"树的高度和深度"的概念。
下面对这几个性质进行简单说明:
[性质一] Bk共有2k个节点。
如上图所示,B0有20=1节点,B1有21=2个节点,B2有22=4个节点,...
[性质二] Bk的高度为k。
如上图所示,B0的高度为0,B1的高度为1,B2的高度为2,...
[性质三] Bk在深度i处恰好有C(k,i)个节点,其中i=0,1,2,...,k。
C(k,i)是高中数学中阶乘元素,例如,C(10,3)=(1098) / (321)=240
B4中深度为0的节点C(4,0)=1
B4中深度为1的节点C(4,1)= 4 / 1 = 4
B4中深度为2的节点C(4,2)= (43) / (21) = 6
B4中深度为3的节点C(4,3)= (432) / (321) = 4
B4中深度为4的节点C(4,4)= (4321) / (4321) = 1
合计得到B4的节点分布是(1,4,6,4,1)。
[性质四] 根的度数为k,它大于任何其它节点的度数。
节点的度数是该结点拥有的子树的数目。
第2部分 二项堆的介绍
二项堆通常被用来实现优先队列,它堆是指满足以下性质的二项树的集合:
(01) 每棵二项树都满足最小堆性质。即,父节点的关键字 <= 它的孩子的关键字。
(02) 不能有两棵或以上的二项树具有相同的度数(包括度数为0)。换句话说,具有度数k的二项树有0个或1个。
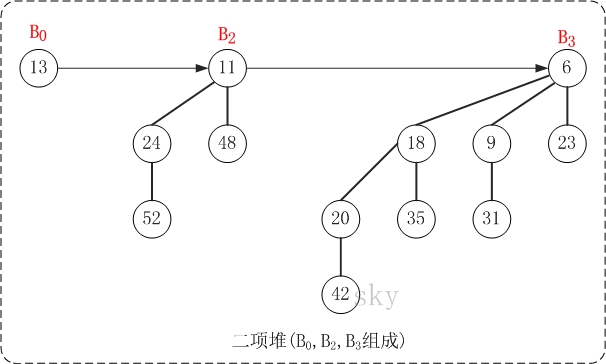
上图就是一棵二项堆,它由二项树B0、B2和B3组成。对比二项堆的定义:(01)二项树B0、B2、B3都是最小堆;(02)二项堆不包含相同度数的二项树。
二项堆的第(01)个性质保证了二项堆的最小节点是某一棵二项树的根节点,第(02)个性质则说明结点数为n的二项堆最多只有log{n} + 1棵二项树。实际上,将包含n个节点的二项堆,表示成若干个2的指数和(或者转换成二进制),则每一个2个指数都对应一棵二项树。例如,13(二进制是1101)的2个指数和为13=23 + 22 + 20, 因此具有13个节点的二项堆由度数为3, 2, 0的三棵二项树组成。
第3部分 二项堆的基本操作
二项堆是可合并堆,它的合并操作的复杂度是O(log n)。
1. 基本定义
public class BinomialHeap<T extends Comparable<T>> {
private BinomialNode<T> mRoot; // 根结点
private class BinomialNode<T extends Comparable<T>> {
T key; // 关键字(键值)
int degree; // 度数
BinomialNode<T> child; // 左孩子
BinomialNode<T> parent; // 父节点
BinomialNode<T> next; // 兄弟节点
public BinomialNode(T key) {
this.key = key;
this.degree = 0;
this.child = null;
this.parent = null;
this.next = null;
}
public String toString() {
return "key:"+key;
}
}
...
}
BinomialNode是二项堆的节点。它包括了关键字(key),用于比较节点大小;度数(degree),用来表示当前节点的度数;左孩子(child)、父节点(parent)以及兄弟节点(next)。
BinomialHeap是二项堆对应的类,它包括了二项堆的根节点mRoot以及二项堆的基本操作的定义。
下面是一棵二项堆的树形图和它对应的内存结构关系图。

2. 合并操作
合并操作是二项堆的重点,它的添加操作也是基于合并操作来实现的。合并两个二项堆,需要的步骤概括起来如下:
(01) 将两个二项堆的根链表合并成一个链表。合并后的新链表按照"节点的度数"单调递增排列。
(02) 将新链表中"根节点度数相同的二项树"连接起来,直到所有根节点度数都不相同。
下面,先看看合并操作的代码;然后再通过示意图对合并操作进行说明。
merge()代码(Java)
/*
* 将h1, h2中的根表合并成一个按度数递增的链表,返回合并后的根节点
*/
private BinomialNode<T> merge(BinomialNode<T> h1, BinomialNode<T> h2) {
if (h1 == null) return h2;
if (h2 == null) return h1;
// root是新堆的根,h3用来遍历h1和h3的。
BinomialNode<T> pre_h3, h3, root=null;
pre_h3 = null;
//整个while,h1, h2, pre_h3, h3都在往后顺移
while ((h1!=null) && (h2!=null)) {
if (h1.degree <= h2.degree) {
h3 = h1;
h1 = h1.next;
} else {
h3 = h2;
h2 = h2.next;
}
if (pre_h3 == null) {
pre_h3 = h3;
root = h3;
} else {
pre_h3.next = h3;
pre_h3 = h3;
}
if (h1 != null) {
h3.next = h1;
} else {
h3.next = h2;
}
}
return root;
}
link()代码(Java)
/*
* 合并两个二项堆:将child合并到root中
*/
private void link(BinomialNode<T> child, BinomialNode<T> root) {
child.parent = root;
child.next = root.child;
root.child = child;
root.degree++;
}
合并操作代码(Java)
/*
* 合并二项堆:将h1, h2合并成一个堆,并返回合并后的堆
*/
private BinomialNode<T> union(BinomialNode<T> h1, BinomialNode<T> h2) {
BinomialNode<T> root;
// 将h1, h2中的根表合并成一个按度数递增的链表root
root = merge(h1, h2);
if (root == null)
return null;
BinomialNode<T> prev_x = null;
BinomialNode<T> x = root;
BinomialNode<T> next_x = x.next;
while (next_x != null) {
if ( (x.degree != next_x.degree)
|| ((next_x.next != null) && (next_x.degree == next_x.next.degree))) {
// Case 1: x.degree != next_x.degree
// Case 2: x.degree == next_x.degree == next_x.next.degree
prev_x = x;
x = next_x;
} else if (x.key.compareTo(next_x.key) <= 0) {
// Case 3: x.degree == next_x.degree != next_x.next.degree
// && x.key <= next_x.key
x.next = next_x.next;
link(next_x, x);
} else {
// Case 4: x.degree == next_x.degree != next_x.next.degree
// && x.key > next_x.key
if (prev_x == null) {
root = next_x;
} else {
prev_x.next = next_x;
}
link(x, next_x);
x = next_x;
}
next_x = x.next;
}
return root;
}
/*
* 将二项堆other合并到当前堆中
*/
public void union(BinomialHeap<T> other) {
if (other!=null && other.mRoot!=null)
mRoot = union(mRoot, other.mRoot);
}
合并函数combine(h1, h2)的作用是将h1和h2合并,并返回合并后的二项堆。在combine(h1, h2)中,涉及到了两个函数merge(h1, h2)和link(child, root)。
merge(h1, h2)就是我们前面所说的"两个二项堆的根链表合并成一个链表,合并后的新链表按照'节点的度数'单调递增排序"。
link(child, root)则是为了合并操作的辅助函数,它的作用是将"二项堆child的根节点"设为"二项堆root的左孩子",从而将child整合到root中去。
在combine(h1, h2)中对h1和h2进行合并时;首先通过 merge(h1, h2) 将h1和h2的根链表合并成一个"按节点的度数单调递增"的链表;然后进入while循环,对合并得到的新链表进行遍历,将新链表中"根节点度数相同的二项树"连接起来,直到所有根节点度数都不相同为止。在将新联表中"根节点度数相同的二项树"连接起来时,可以将被连接的情况概括为4种。
x是根链表的当前节点,next_x是x的下一个(兄弟)节点。
Case 1: x->degree != next_x->degree
即,"当前节点的度数"与"下一个节点的度数"相等时。此时,不需要执行任何操作,继续查看后面的节点。
Case 2: x->degree == next_x->degree == next_x->next->degree
即,"当前节点的度数"、"下一个节点的度数"和"下下一个节点的度数"都相等时。此时,暂时不执行任何操作,还是继续查看后面的节点。实际上,这里是将"下一个节点"和"下下一个节点"等到后面再进行整合连接。
Case 3: x->degree == next_x->degree != next_x->next->degree
&& x->key <= next_x->key
即,"当前节点的度数"与"下一个节点的度数"相等,并且"当前节点的键值"<="下一个节点的度数"。此时,将"下一个节点(对应的二项树)"作为"当前节点(对应的二项树)的左孩子"。
Case 4: x->degree == next_x->degree != next_x->next->degree
&& x->key > next_x->key
即,"当前节点的度数"与"下一个节点的度数"相等,并且"当前节点的键值">"下一个节点的度数"。此时,将"当前节点(对应的二项树)"作为"下一个节点(对应的二项树)的左孩子"。
下面通过示意图来对合并操作进行说明。
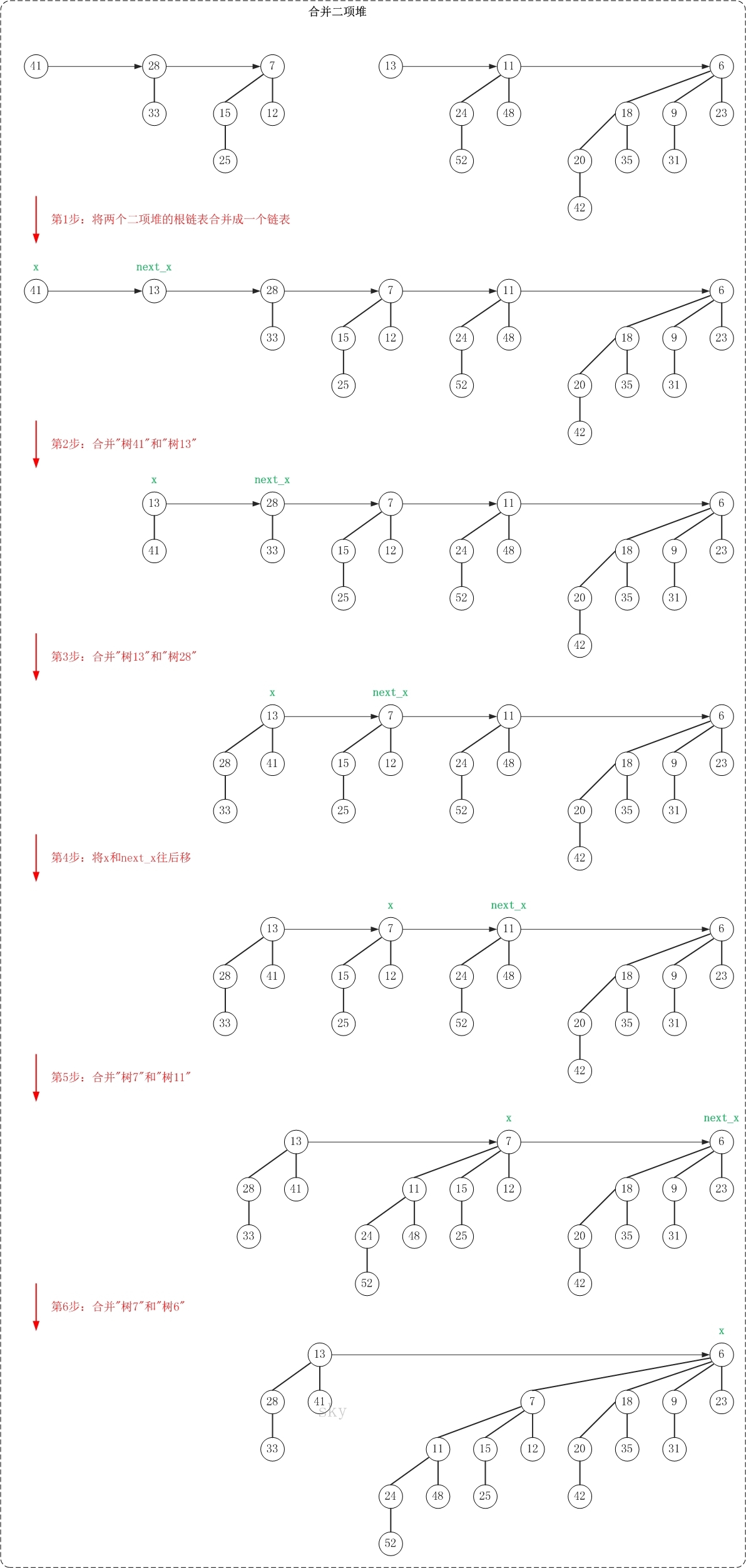
第1步:将两个二项堆的根链表合并成一个链表
执行完第1步之后,得到的新链表中有许多度数相同的二项树。实际上,此时得到的是对应"Case 4"的情况,"树41"(根节点为41的二项树)和"树13"的度数相同,且"树41"的键值 > "树13"的键值。此时,将"树41"作为"树13"的左孩子。
第2步:合并"树41"和"树13"
执行完第2步之后,得到的是对应"Case 3"的情况,"树13"和"树28"的度数相同,且"树13"的键值 < "树28"的键值。此时,将"树28"作为"树13"的左孩子。
第3步:合并"树13"和"树28"
执行完第3步之后,得到的是对应"Case 2"的情况,"树13"、"树28"和"树7"这3棵树的度数都相同。此时,将x设为下一个节点。
第4步:将x和next_x往后移
执行完第4步之后,得到的是对应"Case 3"的情况,"树7"和"树11"的度数相同,且"树7"的键值 < "树11"的键值。此时,将"树11"作为"树7"的左孩子。
第5步:合并"树7"和"树11"
执行完第5步之后,得到的是对应"Case 4"的情况,"树7"和"树6"的度数相同,且"树7"的键值 > "树6"的键值。此时,将"树7"作为"树6"的左孩子。
第6步:合并"树7"和"树6"
此时,合并操作完成!
PS. 合并操作的图文解析过程与"测试程序(Main.java)中的testUnion()函数"是对应的!
3. 插入操作
理解了"合并"操作之后,插入操作就相当简单了。插入操作可以看作是将"要插入的节点"和当前已有的堆进行合并。
插入操作代码(Java)
/*
* 新建key对应的节点,并将其插入到二项堆中。
*/
public void insert(T key) {
BinomialNode<T> node;
// 禁止插入相同的键值
if (contains(key)==true) {
System.out.printf("insert failed: the key(%s) is existed already!\n", key);
return ;
}
node = new BinomialNode<T>(key);
if (node==null)
return ;
mRoot = union(mRoot, node);
}
在插入时,首先通过contains(key)查找键值为key的节点。存在的话,则直接返回;不存在的话,则新建BinomialNode对象node,然后将node和heap进行合并。
注意:我这里实现的二项堆是"进制插入相同节点的"!若你想允许插入相同键值的节点,则屏蔽掉插入操作中的contains(key)部分代码即可。
4. 删除操作
删除二项堆中的某个节点,需要的步骤概括起来如下:
(01) 将"该节点"交换到"它所在二项树"的根节点位置。方法是,从"该节点"不断向上(即向树根方向)"遍历,不断交换父节点和子节点的数据,直到被删除的键值到达树根位置。
(02) 将"该节点所在的二项树"从二项堆中移除;将该二项堆记为heap。
(03) 将"该节点所在的二项树"进行反转。反转的意思,就是将根的所有孩子独立出来,并将这些孩子整合成二项堆,将该二项堆记为child。
(04) 将child和heap进行合并操作。
下面,先看看删除操作的代码;再进行图文说明。
删除操作代码(Java)
/*
* 删除节点:删除键值为key的节点
*/
private BinomialNode<T> remove(BinomialNode<T> root, T key) {
if (root==null)
return root;
BinomialNode<T> node;
// 查找键值为key的节点
if ((node = search(root, key)) == null)
return root;
// 将被删除的节点的数据数据上移到它所在的二项树的根节点
BinomialNode<T> parent = node.parent;
while (parent != null) {
// 交换数据
T tmp = node.key;
node.key = parent.key;
parent.key = tmp;
// 下一个父节点
node = parent;
parent = node.parent;
}
// 找到node的前一个根节点(prev)
BinomialNode<T> prev = null;
BinomialNode<T> pos = root;
while (pos != node) {
prev = pos;
pos = pos.next;
}
// 移除node节点
if (prev!=null)
prev.next = node.next;
else
root = node.next;
root = union(root, reverse(node.child));
// help GC
node = null;
return root;
}
public void remove(T key) {
mRoot = remove(mRoot, key);
}
remove(key)的作用是删除二项堆中键值为key的节点,并返回删除节点后的二项堆。
下面通过示意图来对删除操作进行说明(删除二项堆中的节点20)。
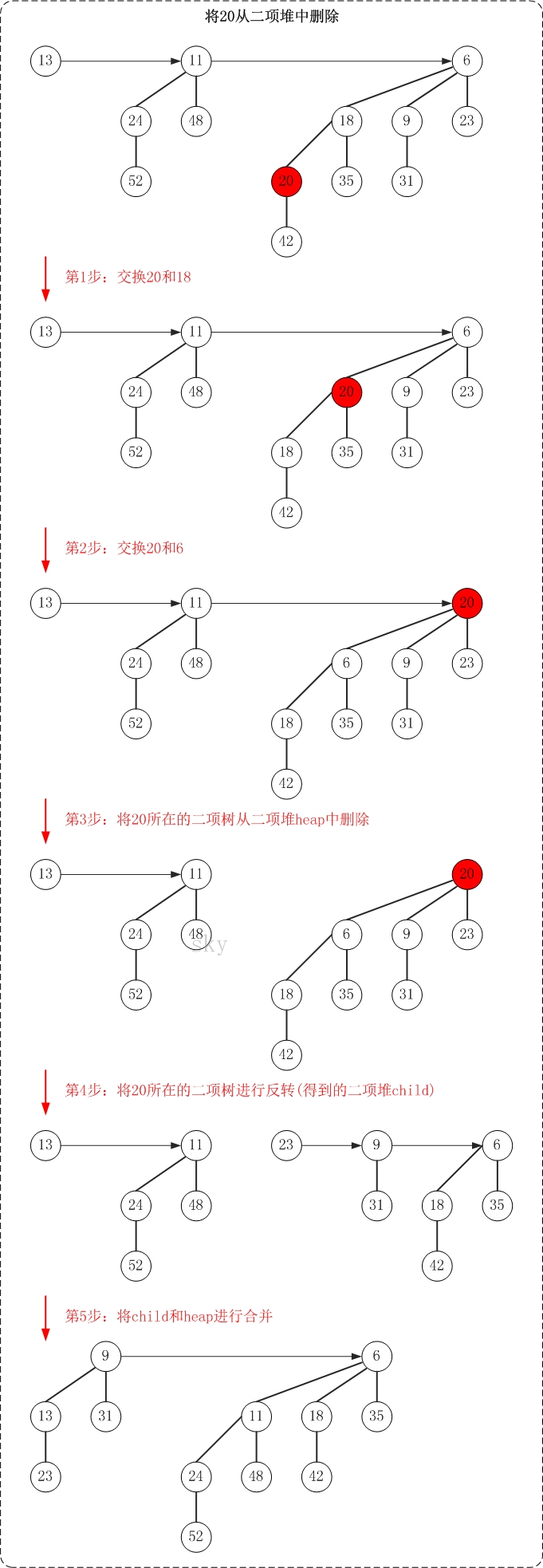
总的思想,就是将被"删除节点"从它所在的二项树中孤立出来,然后再对二项树进行相应的处理。
PS. 删除操作的图文解析过程与"测试程序(Main.java)中的testDelete()函数"是对应的!
5. 更新操作
更新二项堆中的某个节点,就是修改节点的值,它包括两部分分:"减少节点的值" 和 "增加节点的值" 。
更新操作代码(Java)
/*
* 更新二项堆的节点node的键值为key
*/
private void updateKey(BinomialNode<T> node, T key) {
if (node == null)
return ;
int cmp = key.compareTo(node.key);
if(cmp < 0) // key < node.key
decreaseKey(node, key);
else if(cmp > 0) // key > node.key
increaseKey(node, key);
else
System.out.println("No need to update!!!");
}
/*
* 将二项堆中键值oldkey更新为newkey
*/
public void update(T oldkey, T newkey) {
BinomialNode<T> node;
node = search(mRoot, oldkey);
if (node != null)
updateKey(node, newkey);
}
5.1 减少节点的值
减少节点值的操作很简单:该节点一定位于一棵二项树中,减小"二项树"中某个节点的值后要保证"该二项树仍然是一个最小堆";因此,就需要我们不断的将该节点上调。
减少操作代码(Java)
/*
* 减少关键字的值:将二项堆中的节点node的键值减小为key。
*/
private void decreaseKey(BinomialNode<T> node, T key) {
if(key.compareTo(node.key)>=0 || contains(key)==true) {
System.out.println("decrease failed: the new key("+key+") is existed already, or is no smaller than current key("+node.key+")");
return ;
}
node.key = key;
BinomialNode<T> child, parent;
child = node;
parent = node.parent;
while(parent != null && child.key.compareTo(parent.key)<0) {
// 交换parent和child的数据
T tmp = parent.key;
parent.key = child.key;
child.key = tmp;
child = parent;
parent = child.parent;
}
}
下面是减少操作的示意图(20->2)
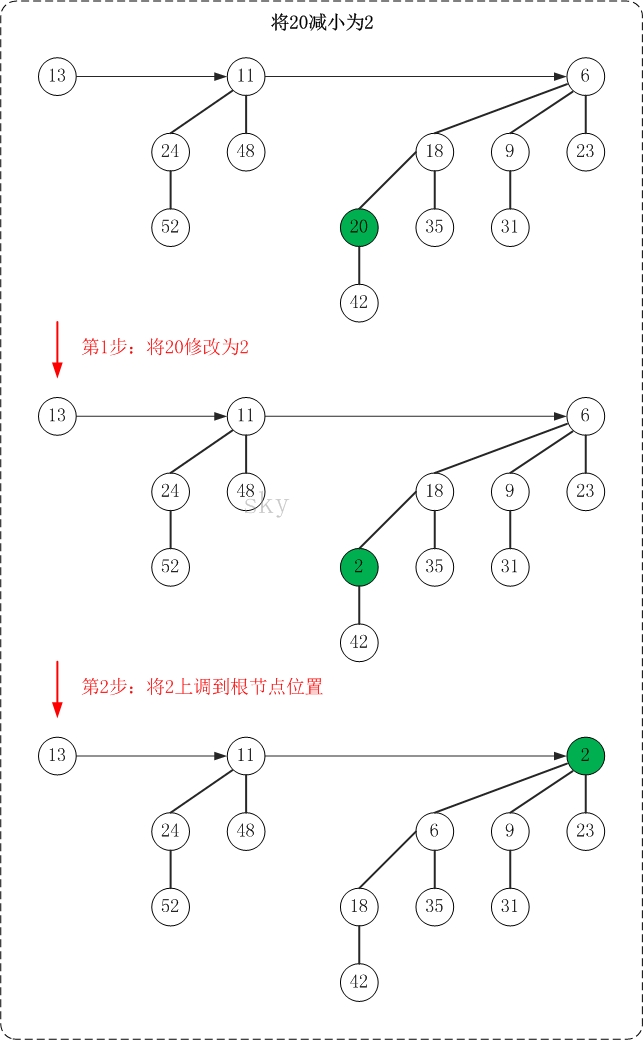
减少操作的思想很简单,就是"保持被减节点所在二项树的最小堆性质"。
PS. 减少操作的图文解析过程与"测试程序(Main.java)中的testDecrease()函数"是对应的!
5.2 增加节点的值
增加节点值的操作也很简单。上面说过减少要将被减少的节点不断上调,从而保证"被减少节点所在的二项树"的最小堆性质;而增加操作则是将被增加节点不断的下调,从而保证"被增加节点所在的二项树"的最小堆性质。
增加操作代码(Java)
/*
* 增加关键字的值:将二项堆中的节点node的键值增加为key。
*/
private void increaseKey(BinomialNode<T> node, T key) {
if(key.compareTo(node.key)<=0 || contains(key)==true) {
System.out.println("increase failed: the new key("+key+") is existed already, or is no greater than current key("+node.key+")");
return ;
}
node.key = key;
BinomialNode<T> cur = node;
BinomialNode<T> child = cur.child;
while (child != null) {
if(cur.key.compareTo(child.key) > 0) {
// 如果"当前节点" < "它的左孩子",
// 则在"它的孩子中(左孩子 和 左孩子的兄弟)"中,找出最小的节点;
// 然后将"最小节点的值" 和 "当前节点的值"进行互换
BinomialNode<T> least = child; // least是child和它的兄弟中的最小节点
while(child.next != null) {
if (least.key.compareTo(child.next.key) > 0)
least = child.next;
child = child.next;
}
// 交换最小节点和当前节点的值
T tmp = least.key;
least.key = cur.key;
cur.key = tmp;
// 交换数据之后,再对"原最小节点"进行调整,使它满足最小堆的性质:父节点 <= 子节点
cur = least;
child = cur.child;
} else {
child = child.next;
}
}
}
下面是增加操作的示意图(6->60)
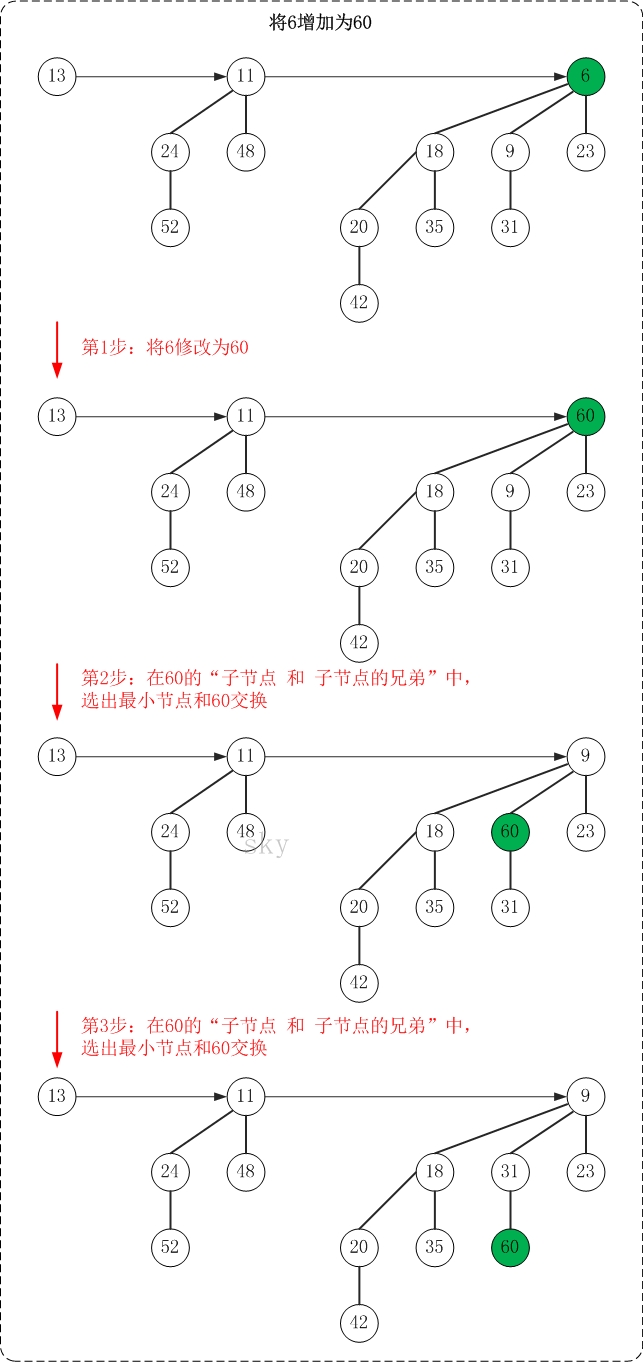
增加操作的思想很简单,"保持被增加点所在二项树的最小堆性质"。
PS. 增加操作的图文解析过程与"测试程序(Main.java)中的testIncrease()函数"是对应的!
注意:关于二项堆的"查找"、"更新"、"打印"等接口就不再单独介绍了,后文的源码中有给出它们的实现代码。有兴趣的话,Please RTFSC(Read The Fucking Source Code)!
第4部分 二项堆的Java实现(完整源码)
点击查看:源代码
二项堆的测试程序包括了五部分,分别是"插入"、"删除"、"增加"、"减少"、"合并"这5种功能的测试代码。默认是运行的"插入"功能代码,你可以根据自己的需要来对相应的功能进行验证!
下面是插入功能运行结果:
== 二项堆(ha)中依次添加: 12 7 25 15 28 33 41
== 二项堆(ha)的详细信息:
== 二项堆( B0 B1 B2 )的详细信息:
1. 二项树B0:
41(0) is root
2. 二项树B1:
28(1) is root
33(0) is 28's child
3. 二项树B2:
7(2) is root
15(1) is 7's child
25(0) is 15's child
12(0) is 15's next