左倾堆(二)之 C++详解

上一章介绍了左倾堆的基本概念，并通过C语言实现了左倾堆。本章是左倾堆的C++实现。

左倾堆的介绍

左倾堆(leftist tree 或 leftist heap)，又被成为左偏树、左偏堆，最左堆等。

它和二叉堆一样，都是优先队列实现方式。当优先队列中涉及到"对两个优先队列进行合并"的问题时，二叉堆的效率就无法令人满意了，而本文介绍的左倾堆，则可以很好地解决这类问题。


左倾堆的定义

左倾堆是一棵二叉树，它的节点除了和二叉树的节点一样具有左右子树指针外，还有两个属性：键值和零距离。

(01) 键值的作用是来比较节点的大小，从而对节点进行排序。
(02) 零距离(英文名NPL，即Null Path Length)则是从一个节点到一个"最近的不满节点"的路径长度。不满节点是指该该节点的左右孩子至少有有一个为NULL。叶节点的NPL为0，NULL节点的NPL为-1。

img

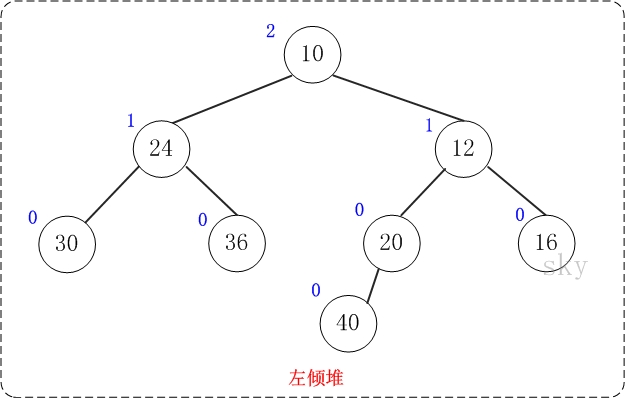
上图是一颗左倾堆，它满足左倾堆的基本性质：

  • [性质1] 节点的键值小于或等于它的左右子节点的键值。
  • [性质2] 节点的左孩子的NPL >= 右孩子的NPL。
  • [性质3] 节点的NPL = 它的右孩子的NPL + 1。


左倾堆，顾名思义，是有点向左倾斜的意思了。它在统计问题、最值问题、模拟问题和贪心问题等问题中有着广泛的应用。此外，斜堆是比左倾堆更为一般的数据结构。当然，今天讨论的是左倾堆，关于斜堆，以后再撰文来表。

前面说过，它能和好的解决"两个优先队列合并"的问题。实际上，左倾堆的合并操作的平摊时间复杂度为O(log n)，而完全二叉堆为O(n)。合并就是左倾树的重点，插入和删除操作都是以合并操作为基础的。插入操作，可以看作两颗左倾树合并；删除操作(移除优先队列中队首元素)，则是移除根节点之后再合并剩余的两个左倾树。闲话说到这里，下面开始介绍左倾树的基本方法。

左倾堆的图文解析

合并操作是左倾堆的重点。合并两个左倾堆的基本思想如下：

  • (01) 如果一个空左倾堆与一个非空左倾堆合并，返回非空左倾堆。
  • (02) 如果两个左倾堆都非空，那么比较两个根节点，取较小堆的根节点为新的根节点。将"较小堆的根节点的右孩子"和"较大堆"进行合并。
  • (03) 如果新堆的右孩子的NPL > 左孩子的NPL，则交换左右孩子。
  • (04) 设置新堆的根节点的NPL = 右子堆NPL + 1


下面通过图文演示合并以下两个堆的过程。

img

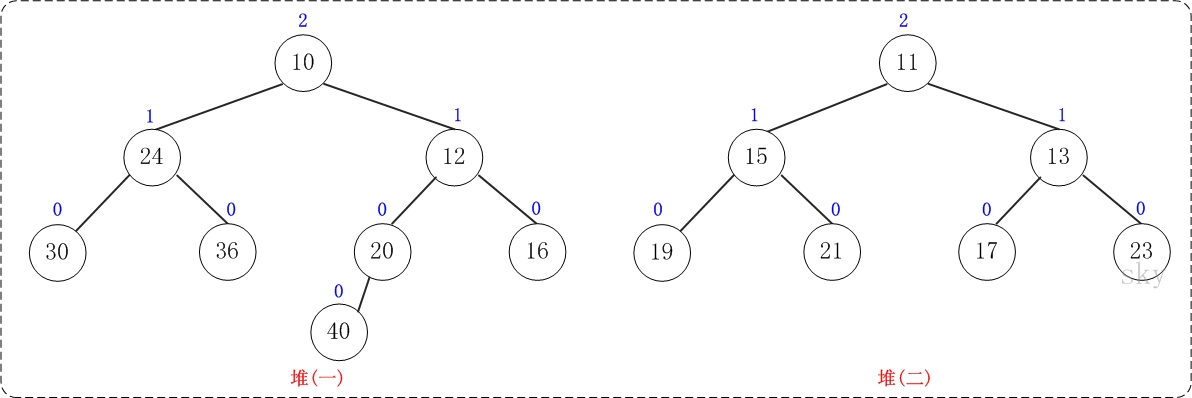
提示：这两个堆的合并过程和源码中的测试程序相对应！

第1步：将"较小堆(根为10)的右孩子"和"较大堆(根为11)"进行合并。

合并的结果，相当于将"较大堆"设置"较小堆"的右孩子，如下图所示：

img

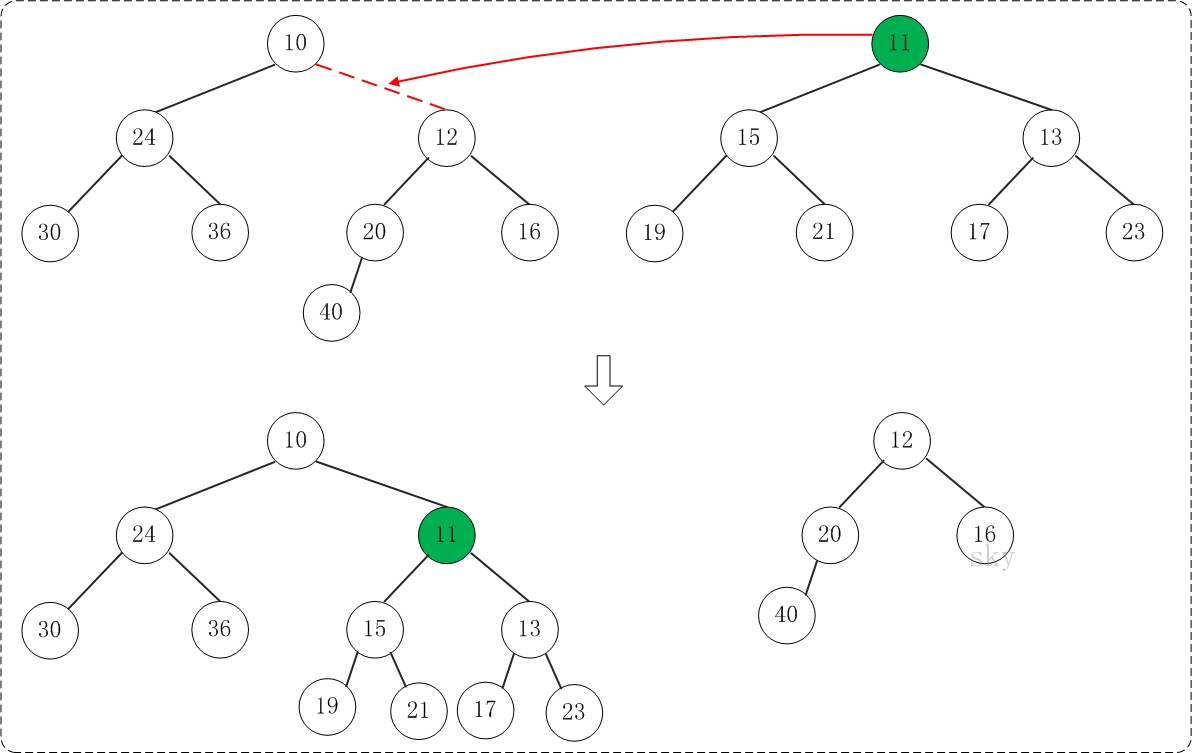
第2步：将上一步得到的"根11的右子树"和"根为12的树"进行合并，得到的结果如下：

img

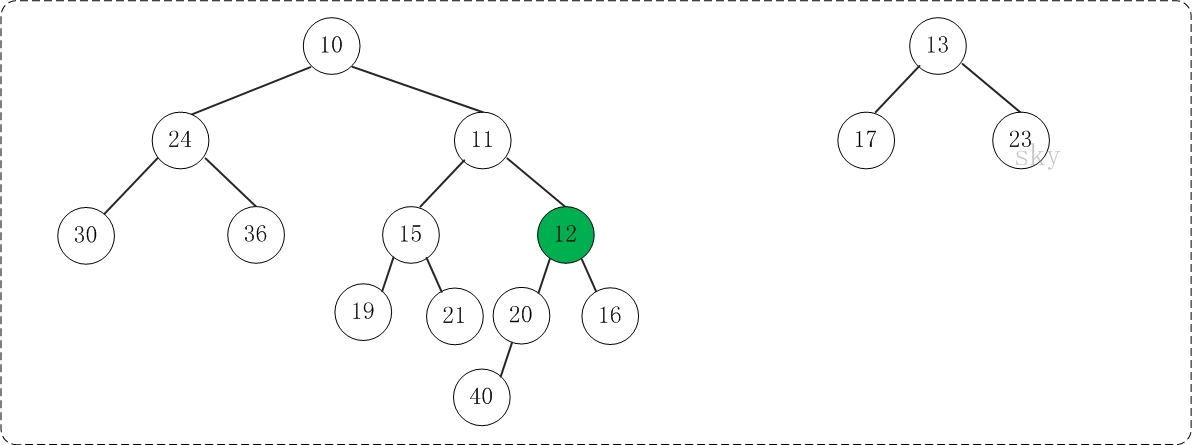
第3步：将上一步得到的"根12的右子树"和"根为13的树"进行合并，得到的结果如下：

img

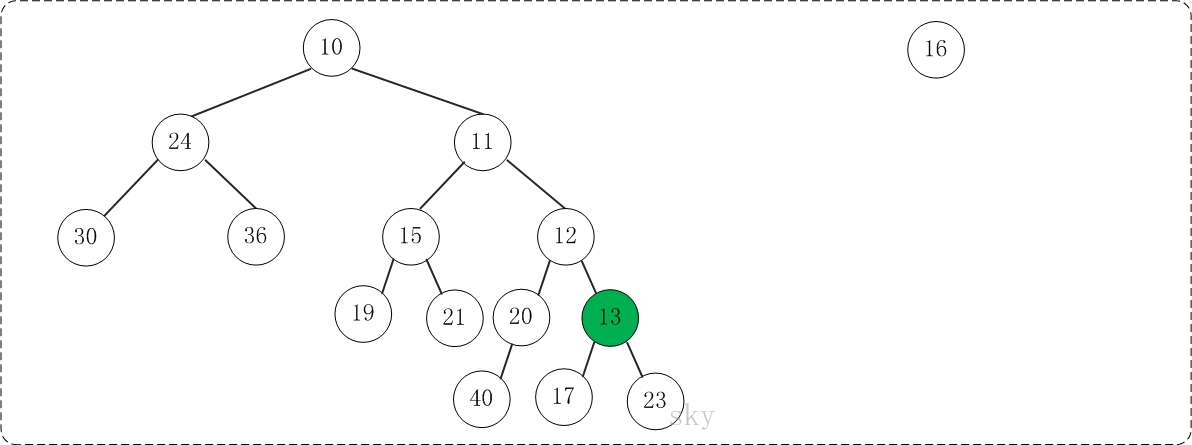
第4步：将上一步得到的"根13的右子树"和"根为16的树"进行合并，得到的结果如下：

img

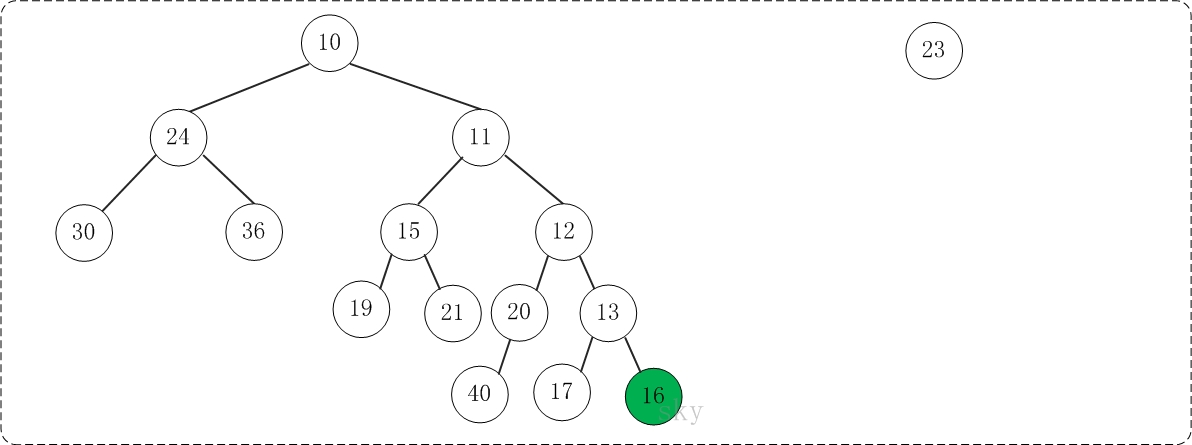
第5步：将上一步得到的"根16的右子树"和"根为23的树"进行合并，得到的结果如下：

img

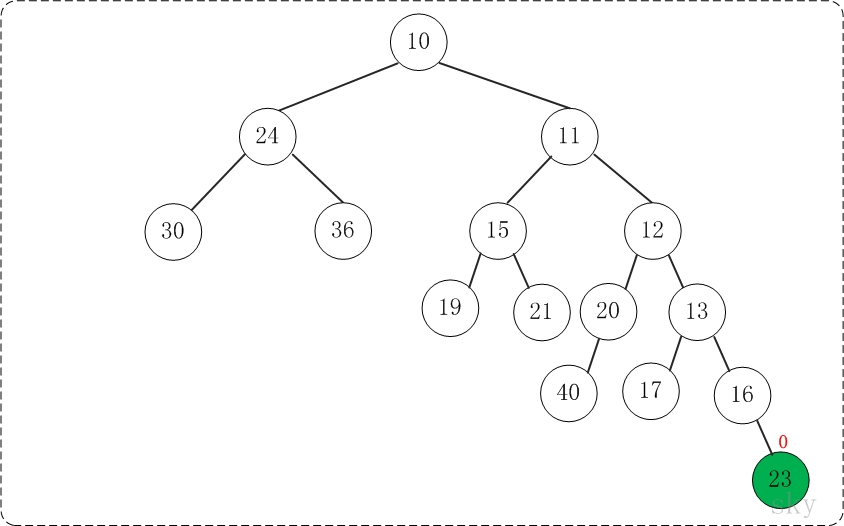
至此，已经成功的将两棵树合并成为一棵树了。接下来，对新生成的树进行调节。

第6步：上一步得到的"树16的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

img

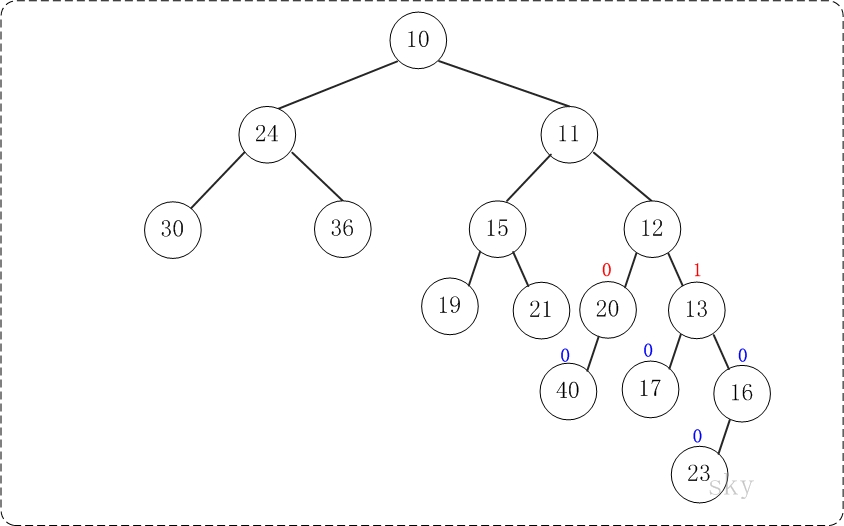
第7步：上一步得到的"树12的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

img

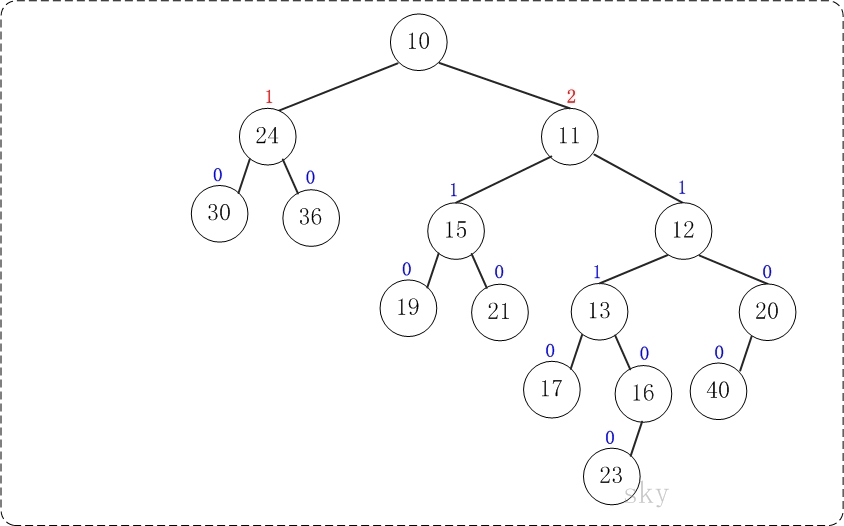
第8步：上一步得到的"树10的右孩子的NPL > 左孩子的NPL"，因此交换左右孩子。得到的结果如下：

img

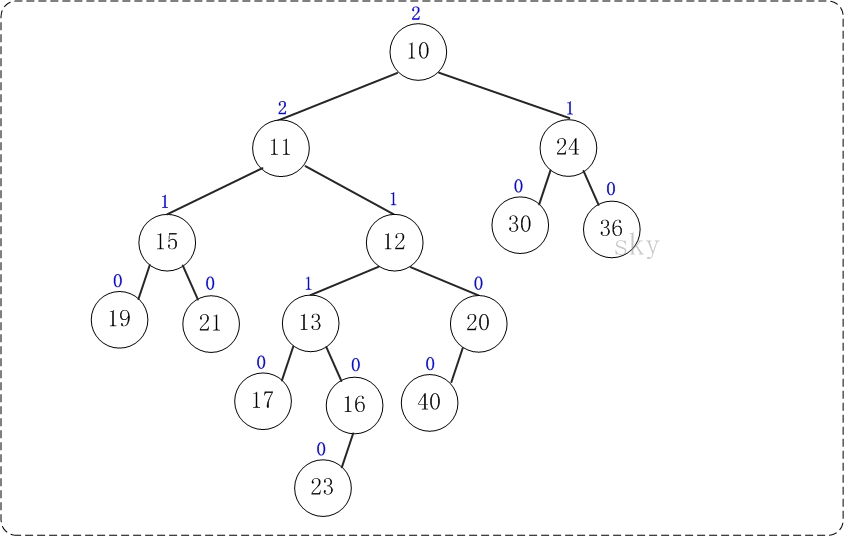
至此，合并完毕。上面就是合并得到的左倾堆！


下面看看左倾堆的基本操作的代码

1. 基本定义

template <class T>
class LeftistNode{
    public:
        T key;              // 关键字(键值)
        int npl;            // 零路经长度(Null Path Length)
        LeftistNode *left;  // 左孩子
        LeftistNode *right; // 右孩子

        LeftistNode(T value, LeftistNode *l, LeftistNode *r):
            key(value), npl(0), left(l),right(r) {}
};

LeftistNode是左倾堆对应的节点类。

template <class T>
class LeftistHeap {
    private:
        LeftistNode<T> *mRoot;  // 根结点

    public:
        LeftistHeap();
        ~LeftistHeap();

        // 前序遍历"左倾堆"
        void preOrder();
        // 中序遍历"左倾堆"
        void inOrder();
        // 后序遍历"左倾堆"
        void postOrder();

        // 将other的左倾堆合并到this中。
        void merge(LeftistHeap<T>* other);
        // 将结点(key为节点键值)插入到左倾堆中
        void insert(T key);
        // 删除结点(key为节点键值)
        void remove();

        // 销毁左倾堆
        void destroy();

        // 打印左倾堆
        void print();
    private:

        // 前序遍历"左倾堆"
        void preOrder(LeftistNode<T>* heap) const;
        // 中序遍历"左倾堆"
        void inOrder(LeftistNode<T>* heap) const;
        // 后序遍历"左倾堆"
        void postOrder(LeftistNode<T>* heap) const;

        // 交换节点x和节点y
        void swapNode(LeftistNode<T> *&x, LeftistNode<T> *&y);
        // 合并"左倾堆x"和"左倾堆y"
        LeftistNode<T>* merge(LeftistNode<T>* &x, LeftistNode<T>* &y);
        // 将结点(z)插入到左倾堆(heap)中
        LeftistNode<T>* insert(LeftistNode<T>* &heap, T key);
        // 删除左倾堆(heap)中的结点(z)，并返回被删除的结点
        LeftistNode<T>* remove(LeftistNode<T>* &heap);

        // 销毁左倾堆
        void destroy(LeftistNode<T>* &heap);

        // 打印左倾堆
        void print(LeftistNode<T>* heap, T key, int direction);
};

LeftistHeap是左倾堆类，它包含了左倾堆的根节点，以及左倾堆的操作。

2. 合并

/*
 * 合并"左倾堆x"和"左倾堆y"
 */
template <class T>
LeftistNode<T>* LeftistHeap<T>::merge(LeftistNode<T>* &x, LeftistNode<T>* &y)
{
    if(x == NULL)
        return y;
    if(y == NULL)
        return x;

    // 合并x和y时，将x作为合并后的树的根；
    // 这里的操作是保证: x的key < y的key
    if(x->key > y->key)
        swapNode(x, y);

    // 将x的右孩子和y合并，"合并后的树的根"是x的右孩子。
    x->right = merge(x->right, y);

    // 如果"x的左孩子为空" 或者 "x的左孩子的npl<右孩子的npl"
    // 则，交换x和y
    if(x->left == NULL || x->left->npl < x->right->npl)
    {
        LeftistNode<T> *tmp = x->left;
        x->left = x->right;
        x->right = tmp;
    }
    // 设置合并后的新树(x)的npl
    if (x->right == NULL || x->left == NULL)
        x->npl = 0;
    else
        x->npl = (x->left->npl > x->right->npl) ? (x->right->npl + 1) : (x->left->npl + 1);

    return x;
}

/*
 * 将other的左倾堆合并到this中。
 */
template <class T>
void LeftistHeap<T>::merge(LeftistHeap<T>* other)
{
    mRoot = merge(mRoot, other->mRoot);
}

merge(x, y)是内部接口，作用是合并x和y这两个左倾堆，并返回得到的新堆的根节点。

merge(other)是外部接口，作用是将other合并到当前堆中。

3. 添加

/* 
 * 将结点插入到左倾堆中，并返回根节点
 *
 * 参数说明：
 *     heap 左倾堆的根结点
 *     key 插入的结点的键值
 * 返回值：
 *     根节点
 */
template <class T>
LeftistNode<T>* LeftistHeap<T>::insert(LeftistNode<T>* &heap, T key)
{
    LeftistNode<T> *node;   // 新建结点

    // 新建节点
    node = new LeftistNode<T>(key, NULL, NULL);
    if (node==NULL)
    {
        cout << "ERROR: create node failed!" << endl;
        return heap;
    }

    return merge(mRoot, node);
}

template <class T>
void LeftistHeap<T>::insert(T key)
{
    mRoot = insert(mRoot, key);
}

insert(heap, key)是内部接口，它是以节点为操作对象的。

insert(key)是外部接口，它的作用是新建键值为key的节点，并将其加入到当前左倾堆中。

4. 删除

/* 
 * 删除结点，返回根节点
 *
 * 参数说明：
 *     heap 左倾堆的根结点
 * 返回值：
 *     根节点
 */
template <class T>
LeftistNode<T>* LeftistHeap<T>::remove(LeftistNode<T>* &heap)
{
    if (heap == NULL)
        return NULL;

    LeftistNode<T> *l = heap->left;
    LeftistNode<T> *r = heap->right;

    // 删除根节点
    delete heap;

    return merge(l, r); // 返回左右子树合并后的新树
}

template <class T>
void LeftistHeap<T>::remove()
{
    mRoot = remove(mRoot);
}

remove(heap)是内部接口，它是以节点为操作对象的。

remove()是外部接口，它的作用是删除左倾堆的最小节点。


PS. 关于左倾堆的"前序遍历"、"中序遍历"、"后序遍历"、"打印"、"销毁"等接口就不再单独介绍了。后文的源码中有给出它们的实现代码，Please RTFSC(Read The Fucking Source Code)！

左倾堆的完整源码

源码共包含2个文件。

  1. 左倾堆的实现文件(LeftistHeap.h)

  2. 左倾堆的测试程序(LeftistHeapTest.cpp)

by skywang
Previous     Next